percentileCont
The percentileCont function calculates percentile based on a continuous distribution of the numbers in the measure. It uses the grouping and sorting that are applied in the field wells. It answers questions like: What values are representative of this percentile? To return an exact percentile value that might not be present in your dataset, use percentileCont. To return the nearest percentile value that is present in your dataset, use percentileDisc instead.
Syntax
percentileCont(expression, percentile, [group-by level])Arguments
measure
Specifies a numeric value to use to compute the percentile. The argument must be a measure or metric. Nulls are ignored in the calculation.
percentile
The percentile value can be any numeric constant 0–100. A percentile value of 50 computes the median value of the measure.
group-by level
(Optional) Specifies the level to group the aggregation by. The level added can be any dimension or dimensions independent of the dimensions added to the visual.
The argument must be a dimension field. The group-by level must be enclosed in square brackets [ ]. For more information, see LAC-A functions.
Returns
The result of the function is a number.
Usage notes
The percentileCont function calculates a result based on a continuous distribution of the values from a specified measure. The result is computed by linear interpolation between the values after ordering them based on settings in the visual. It's different from percentileDisc, which simply returns a value from the set of values that are aggregated over. The result from percentileCont might or might not exist in the values from the specified measure.
Examples of percentileCont
The following examples help explain how percentileCont works.
Example Comparing median, percentileCont, and percentileDisc
The following example shows the median for a dimension (category) by using the median, percentileCont, and percentileDisc functions. The median value is the same as the percentileCont value. percentileCont interpolates a value, which might or might not be in the data set. However, because percentileDisc always displays a value that exists in the dataset, the two results might not match. The last column in this example shows the difference between the two values. The code for each calculated field is as follows:
-
50%Cont = percentileCont( example , 50 )
-
median = median( example )
-
50%Disc = percentileDisc( example , 50 )
-
Cont-Disc = percentileCont( example , 50 ) − percentileDisc( example , 50 )
-
example = left( category, 1 ) (To make a simpler example, we used this expression to shorten the names of categories down to their first letter.)
example median 50%Cont 50%Disc Cont-Disc
-------- ----------- ------------ -------------- ------------
A 22.48 22.48 22.24 0.24
B 20.96 20.96 20.95 0.01
C 24.92 24.92 24.92 0
D 24.935 24.935 24.92 0.015
E 14.48 14.48 13.99 0.49Example 100th percentile as maximum
The following example shows a variety of percentileCont values for the example field. The calculated fields n%Cont are defined as percentileCont( {example} ,n). The interpolated values in each column represent the numbers that fall into that percentile bucket. In some cases, the actual data values match the interpolated values. For example, the column 100%Cont shows the same value for every row because 6783.02 is the highest number.
example 50%Cont 75%Cont 99%Cont 100%Cont
--------- ----------- ----------- ------------ -----------
A 20.97 84.307 699.99 6783.02
B 20.99 88.84 880.98 6783.02
C 20.99 90.48 842.925 6783.02
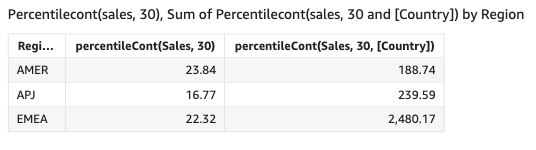
D 21.38 85.99 808.49 6783.02 You can also specify at what level to group the computation using one or more dimensions in the view or in your dataset. This is called a LAC-A function. For more information about LAC-A functions, see LAC-A functions. The following example calculates the 30th percentile based on a continuous distribution of the numbers at the Country level, but not across other dimensions (Region) in the visual.
percentileCont({Sales}, 30, [Country])